三维图形矩阵变换

前言

由于我是从事医疗行业软件开发的，所以必不可少的会和图像打交道，最近刚刚好在做一个图像旋转相关的功能，借此又复习（预习）了一下线性代数，趁着没忘赶紧做一下笔记。

DICOM 中与方位计算有关的 Tag

在开始之前，有必要先了解一下DICOM中与图像方位计算有关的几个Tag，主要有3个。

Tag	Keyword
(0020,0032)	Image Position (Patient)
(0020,0037)	Image Orientation (Patient)

其中Image Position指的是图像左上角的像素在患者坐标系中的位置。 Image Orientation由6个数字组成，分别是图像的行(Row)方向和列(Column)方向的单位向量与x/y/z坐标轴夹角的余弦值(cosine)。

有了上面两个Tag的值，就可以计算出图像在空间坐标系中的位置和方位了。

计算法向量

现在我们已经有了图像平面上两个垂直的向量，行和列方向的向量，使用行列式就能计算出图像所在平面的法向量了。

$$u × v = \left[\begin{matrix} i & j & k \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{matrix}\right]$$

具体怎么算，可以看这里，讲得很详细。

代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
double[] vector1 = new[] {orientation[0], orientation[1], orientation[2]};
double[] vector2 = new[] {orientation[3], orientation[4], orientation[5]};

double[] normal = new double[] { 0, 0, 0 };

normal[0] = vector1[1] * vector2[2] - vector1[2] * vector2[1];
normal[1] = vector1[2] * vector2[0] - vector1[0] * vector2[2];
normal[2] = vector1[0] * vector2[1] - vector1[1] * vector2[0];

var temp = Math.Sqrt(normal[0] * normal[0] + normal[1] * normal[1] + normal[2] * normal[2]);

normal[0] /= temp;
normal[1] /= temp;
normal[2] /= temp;

其中orientation就是Image Orientation中的6个值。计算得到的normal就是图像所在平面的法向量的单位向量。

图像方位矩阵

在3D图形变换中经常使用的是4维矩阵，把图像的位置信息也放到矩阵中，可以方便的进行位置变换的计算。

这里分别用u，v，w表示图像的行/列/法线方向向量，S代表图像位置。

$$u=(u_1,u_2,u_3)$$ $$v=(v_1,v_2,v_3)$$ $$w=(w_1,w_2,w_3)$$ $$S=(s_x,s_y,s_z)$$

4维矩阵则表示为

$$matrix=\left[\begin{matrix} u_1 & v_1 & w_1 & s_x \\ u_2 & v_2 & w_2 & s_y \\ u_3 & v_3 & w_3 & s_z \\ 0 & 0 & 0 & 1 \end{matrix}\right]$$

图像旋转

先来看特殊情况下的旋转，即矩阵绕坐标轴的旋转。T为变换矩阵。

绕X轴旋转
$$T=\left[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & cos\theta & -sin\theta & 0 \\ 0 & sin\theta & cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right]$$
绕Y轴旋转
$$T=\left[\begin{matrix} cos\theta & 0 & sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -sin\theta & 0 & cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right]$$
绕Z轴旋转
$$T=\left[\begin{matrix} cos\theta & -sin\theta & 0 & 0 \\ sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right]$$

直接用$matrix \times T$就可以得到旋转后的矩阵了。

但是图像旋转并不一定是绕坐标轴旋转，这里说图像旋转指的是在图像所在平面上的旋转，即图像矩阵绕法线旋转一定角度，不存在其它情况，所以需要一种更加通用的计算方法。角度的正负按右手定则决定。

经测试，下面的方法并不通用，下面的旋转矩阵适用于点位置的变换，不适用于DICOM中的方位变换

~~这里直接给出结果，图像矩阵绕向量$(u,v,w)$旋转$\theta$的变换矩阵T。~~

$$T=\left[\begin{matrix} u^2+(1-u^2)cos\theta & u v(1-cos\theta)-w sin\theta & u w(1-cos\theta)+v sin\theta & 0 \\ u v(1-cos\theta)+w sin\theta & v^2+(1-v^2)cos\theta & v w(1-cos\theta)-u sin\theta & 0 \\ u w(1-cos\theta)-v sin\theta & v w(1-cos\theta)+u sin\theta & w^2+(1-w^2)cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{matrix}\right]$$

~~代码示例：~~

~~这里用到了MatrixD，主要是用于矩阵的运算。~~

这里其实是我想的复杂了，DICOM图像旋转的本质就是两个方向向量的旋转，只需要将两个方向向量绕法向量旋转即可。而这一切fo-dicom都已经为我们做好了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
Vector3D forward = new Vector3D(new[] { orientation[0], orientation[1], orientation[2] });
Vector3D down = new Vector3D(new[] { orientation[3], orientation[4], orientation[5] });

Orientation3D orientation3D = new Orientation3D(forward, down);

// 旋转，顺时针为正，逆时针为负
orientation3D.Pitch(angle * Math.PI / 180.0);

// orientation3D.Forward
// orientation3D.Down

实现起来很简单，浏览Pitch的源码就会发现，其实就是将两个向量绕Right向量（即法向量）旋转，得到新的Forward和Down就是旋转后图像的方位信息。

这里借一张图来说明问题：

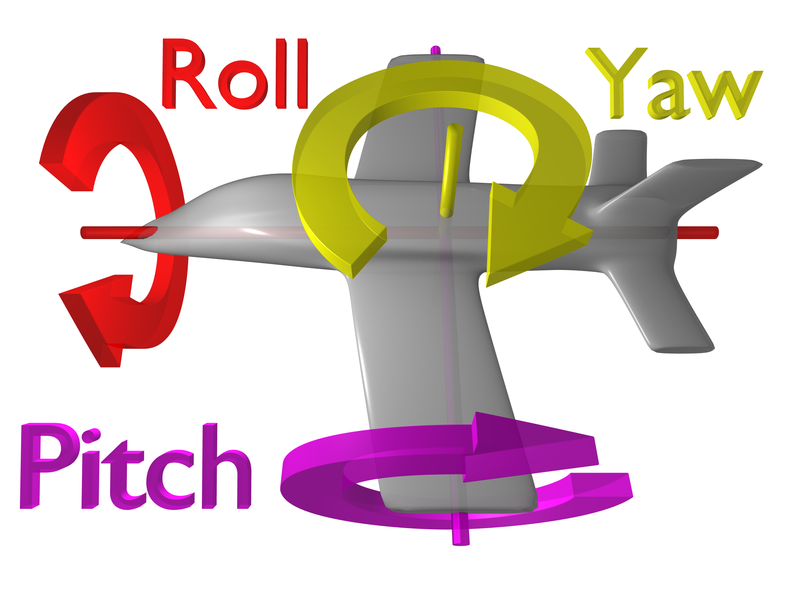
yaw-roll-pitch

在创建Orientation3D时的参数Forward和Down就是图像的行方向和列方向的方向向量，Pitch方法将Forward和Down向量旋转一个角度，得到的就是旋转后图像的行和列的方向向量。

图像翻转

翻转后的方位计算则比较简单，如果是水平翻转，只需要将水平(Row)方向的向量反向即可，竖直翻转将竖直(Column)方向的向量反向即可。

向量反向只需要将 (u,v,w) 3个值前面添加负号即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
// 水平翻转
var newOrientation = new double[6]
{
    -orientation[0], -orientation[1], -orientation[2],
    orientation[3], orientation[4], orientation[5]
};
// 竖直翻转
var newOrientation = new double[6]
{
    orientation[0], orientation[1], orientation[2],
    -orientation[3], -orientation[4], -orientation[5]
};

不过，像这么奇葩的功能应该不会有人去用吧。

注意

对图像矩阵进行旋转或者翻转操作之后，由于图像左上角的像素已经发生变化，所以原有的位置信息也已经改变，需要重新计算才能保证图像在空间中处于正确的位置。对于图像翻转来说或许能够轻易计算出来，不过旋转之后的图像却比较难计算了。

最后，附上一段计算图像方位的代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// [R] Right - 沿着X方向递减
// [L] Left - 沿着X方向递增
// [A] Anterior - 沿着Y方向递减
// [P] Posterior - 沿着Y方向递增
// [F] Feet - 沿着Z方向递减
// [H] Head - 沿着Z方向递增
static string ComputeOrientation(Vector3D vector)
{
    char x = vector.X < 0 ? 'R' : 'L';
    char y = vector.Y < 0 ? 'A' : 'P';
    char z = vector.Z < 0 ? 'F' : 'H';

    double x1 = Math.Abs(vector.X);
    double y1 = Math.Abs(vector.Y);
    double z1 = Math.Abs(vector.Z);

    string result = "";

    for (int i = 0; i < 3; i++)
    {
        if (x1 > 0.0001 && x1 > y1 && x1 > z1)
        {
            result += x;
            x1 = 0;
        }
        else if (y1 > 0.0001 && y1 > x1 && y1 > z1)
        {
            result += y;
            y1 = 0;
        }
        else if (z1 > 0.0001 && z1 > x1 && z1 > y1)
        {
            result += z;
            z1 = 0;
        }
        else
        {
            break;
        }
    }

    return result;
}